Jednou z najdôležitejších ekologických tém na svete je ochrana rôznych typov ekosystémov. Nelichotivá situácia v tejto oblasti je napríklad v krajine s veľmi bohatým ekologickým potenciálom, v Chile. Preto členovia Transdisciplinárneho výskumného centra pre sociálne a ekologické stratégie pre trvalo udržateľné obhospodarovanie lesov v Južnej Amerike na Universidad Austral de Chile vydali koncom roka 2018 výzvu pre výskumných pracovníkov z celého sveta, ktorí by prispeli k riešeniu tohto stavu. Do výzvy sa zapojil aj Mgr. Jozef Kiseľák, PhD. z Ústavu matematických vied PF UPJŠ, v spolupráci s matematikmi z Rakúska a Českej republiky. Výsledkom je štúdia, ktorá je súčasťou jednej z najviac používaných SpringerLink monografií.
Autori sa vo svojej prípadovej štúdii sústredili na analýzu stavu mokradí v Chile. Tieto ekosystémy sú ukážkovým príkladom biodiverzity. Napriek tomu, že sú jedným z prirodzených producentov skleníkových plynov (oxidu uhličitého a metánu), ubúdanie týchto ekosystémov môže mať nepriaznivé následky na našu planétu. Použitím štatisticko-analytických metód autori vyhodnocovali ekologickú zraniteľnosť (ecological vulnerability – EV), ktorá je významná pre ochranu a podporu stability ekosystému. Z matematického pohľadu je ekosystém dynamickým komplexným systémom meniacim sa v čase, na ktorý sa môžeme dívať ako na tzv. časový rad. S tým súvisia výskumné prístupy, ktoré môžeme pri štúdiu ekosystému použiť. Teoretickým východiskom spomínaných autorov bola rekurenčná analýza, pozri Obrázok 1.
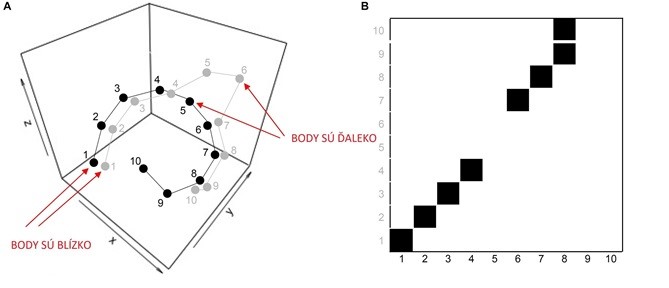
Obrázok 1: Rekurenčný graf ukazuje, či sú jednotlivé stavy dynamického systému rekonštruované z daného časového radu ‘’blízke’’: ak áno (ako napr. dvojica bodov čierna 4 a sivá 4 na obr. A), priradí sa tejto dvojici čierny štvorček na obr. B, ak nie (ako napr. dvojica bodov čierna 5 a sivá 5), priradí sa jej biely štvorček. Výsledný vzor výskytu týchto stavov zaznamenaných na rekurenčnom grafe na obr. B poskytuje dôležité informácie o správaní sa skúmaného systému
Ukazuje sa, že tieto teoretické východiská dávajú v praxi dobré výsledky. Autori ich overili na nameraných hodnotách emisií metánu a oxidu uhličitého v mokradiach v južnom Česku. Výsledky dobre odpovedali správaniu sa ekosystému. Namerané hodnoty a rekurenčný graf poukazujú na fakt, že je tu prítomná výrazná náhodná zložka podobná autoregresným náhodným procesom a tiež o čosi menej výrazná chaotická zložka podobná nelineárnej logistickej iterácii. Výsledky rekurenčnej analýzy, viď. Obrázok 2, napomáhajú detegovať štrukturálne zmeny v dynamike systému, akými sú napríklad prechody typu periodicita-chaos, či chaos-chaos.
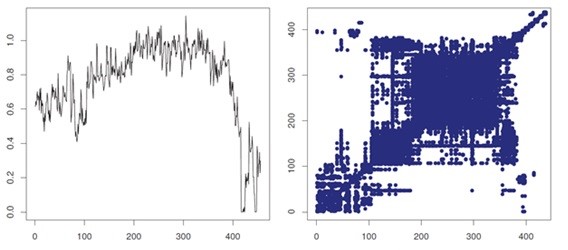
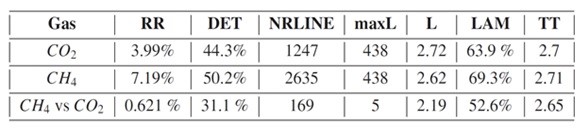
Obrázok 2: Jeden časový úsek nameraných dát metánu, zodpovedajúci rekurenčný graf a výsledky rekurenčnej analýzy (tabuľka). Izolované body odrážajú náhodné správanie (silná fluktuácia v procese). Hodnoty DET (percento rekurenčných bodov, ktoré tvoria diagonálne línie), ktoré sú indikátorom determinizmu v skúmanom systéme, nie sú príliš vysoké, čo potvrdzuje, že aj stochastická časť je prítomná vo výraznej miere. Vertikálne a horizontálne klastre (vysoké percentuálne hodnoty LAM) znamenajú, že niektoré stavy sa určitý čas nezmenia alebo sa menia pomaly (indikácia laminárnych stavov systému).
Publikované štatistické výstupy poskytujú prínosné informácie, ktoré môžu pomôcť zaujať správny postoj k ochrane mokraďových ekosystémov a na základe toho príjmať vhodné opatrenia k regulácii skleníkových plynov.
Odkaz na publikované štúdie:
Stehlík M., Kiseľák J., Dušek J. (2020) On Ecosystem Dynamics for the Conservation of Wetlands and Forest. In: Fuders F., Donoso P. (eds) Ecological Economic and Socio Ecological Strategies for Forest Conservation. Springer, Cham. https://link.springer.com/chapter/10.1007/978-3-030-35379-7_9
Kiseľák J., Dušek J., Stehlík M. (2018). Recurrence of CH4 and CO2 emissions measured by a non-steady state flow-through chamber system. AIP Conference Proceedings, 2046, 020046. https://aip.scitation.org/doi/10.1063/1.5081566










